Chapter 3: Worksheet 4 Jack K. Cohen Colorado School of Mines
Techniques of Differentiation: Chain Rule
Suggested Problems
Section 3.3: See below.
The chain rule is vital. You absolutely must drill this until you can perform it on automatic pilot. Again use to check your work. Some additional commands that may be helpful are Expand and Factor. Try Expand[(1 + 2x)ˆ12] followed by Factor[%] to get the idea. And don't forget Simplify.
- Do problems 2, 4, 6, 8,12, 14, 16, 22, 24, 38, 40, 42, 44.
- Use the fact that
D sin x = cos x to find the derivatives of the following functions:
- sin x3 (Recall that this notation means
sin(x3))
- sin3x (Recall that this notation means
(sin x)3)
-
sin(sin x)
-
sin(sin(sin x))
- Let A be the area of a circle of radius r.
- Express
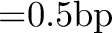 as a function of r and
as a function of r and
 .
.
- (3.3.49)At what rate is the area of a circle increasing when its radius is 10 cm and is increasing at the rate of 2 cm/sec?
- Express
 as a function of A and
as a function of A and
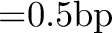 .
.
- (3.3.50)At what rate is the radius of a circle decreasing when its area is 75π cm2 and is decreasing at the rate of 2π cm2/sec?
- Suppose that the rate of change of the volume of a sphere is proportional its surface area.
- Prove that the rate of change of its radius is a constant c.
- If the radius has length r0 at t = t0, what is the radius r at other times t?
- Does your formula for r ``work'' if c < 0 and t is very large?
- (3.3.61) A spherical snowball is melting in such a way that the rate of decrease of its volume is proportional to its surface area. At 10 A.M. its volume was 500 cm3, and at 11 A.M. its volume was 250 cm3. When did the snowball finish melting?
- Suppose that the rate of change of the volume of a cube is proportional its surface area.
- Prove that the rate of change of its edge is a constant c.
- If the edge has length e0 at t = t0, what is its length e at other times t?
- (3.3.62) A cubical block of ice with edge 20 cm begins to melt at 8 A.M. Each edge decreases steadily thereafter, and at 4 P.M. is 8 cm. What was the rate of change of the volume of the block of ice at 12 noon?
- (3.3.36) Use to compute the derivative of
G(x) = {1 + [x + (x2 + x3)4]5}6. Try out each of Simplify[G'[x]], Factor[G'[x]], and Expand[G'[x]]. Don't hand in your results!
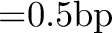 as a function of r and
as a function of r and
 .
.
 as a function of A and
as a function of A and
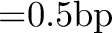 .
.